quant-ratio-proportion-theory-part1

Ratio & Proportion

Ratio:

If the values of two quantities A and B are 4 and 6 respectively, then we say that they are in the ratio 4 : 6 (read as “four is to six”). Ratio is the relation which one quantity bears to another of the same kind, the comparison being made by considering what multiple, part or parts, one quantity is of the other. The ratio of two quantities “a” and “b” is represented as a : b and read as “a is to b”. Here, “a” is called antecedent, “b” is the consequent. Since the ratio expresses the number of times one quantity contains the other, it’s an abstract quantity.

Ratio of any number of quantities is expressed after removing any common factors that all the terms of the ratio have. For example, if there are two quantities having values of 4 and 6, their ratio is 4 : 6 i.e., 2 : 3 after taking the common factor 2 between them out. Similarly, if there are three quantities 6, 8 and 18, there is a common factor between all three of them. So, dividing each of the three terms by 2, we get ratio as 3 : 4 : 9.

If two quantities whose values are A and B respectively ire in the ratio a : b, since we know that some common factor k(>0) would have been removed from A and B to *the ratio a b we can write the original values of the two quantities (i.e., A and B) as ak and bk respectively For example, if the salaries of two persons are in ratio 7 : 5, we can write their individual salaries as 7k and 5k respectively.

A ratio a : b can also be expressed as a/b. So if two items are in the ratio 2 : 3 we can say that their ratio is 2/3. If two terms are in the ratio 2, it means that they are in the ratio of 2/1, i.e., 2 : 1

“A ratio is said to be a ratio of greater or less inequality or of equality according as antecedent is greater than, less than or equal to consequent”. In other words,

- the ratio a : b where a > b is called a ratio of greater inequality (example 3 : 2)

- the ratio a : b where a b is called a ratio of less inequality (example 3 : 5)

- the ratio a : b where a b is called a ratio of equality (example 1 :1)

From this we can find that a ratio of greater inequality is diminished and a ratio of less inequality is increased by adding same quantity to both terms, i.e., in the ratio a b, when we add the same quantity x (positive) to both the terms of the ratio, we have the following results

if a < b then (a + x) : (b + x) > a : b

if a > b then (a + x) : (b + x) < a : b

if a = b then (a + x) : (b + x) = a : b

This idea can also be helpful in questions on Data interpretation when we need to compare fractions to find the larger of two given fractions.

If two quantities are in the ratio a b, then the first quantity will be a + a times the total of the two quantity and the second quantity will be equal to b + b times the total of the two quantities.

• The compounded ratio of ratios A B and C : D is A x C : B x D
• The compounded ratio of ratios A : B, C : D and E : F is ACE : BDF
• The duplicate ratio of A : B is A2 : B2
• The triplicate ratio of A : B is A3 : B3
• The sub duplicate ratio of A : B is
• The sub triplicate ratio of A : B is
• The inverse ratio of A : B = B : A

If A : B = C : D, then

• B : A = D : C. This property is called Invertendo.
• A : C = B : D This property is called Alternendo:
• A + B : B = C + D : D. This property is called Componendo.
• A – B : B = C – D : D. This property is called Dividendo
• A + B : A – B = C + D : C - D. This property is called Componendo - Dividendo.

Equal Ratios

If , then each ratio is equal to

If , then each ratio is equal to

SOLVED EXAMPLES

Example 1.The salaries of David and John are in the ratio of 5 : 9, The sum of their salaries is Rs.35000. Find their individual salaries?

Solution:Since the ratio is 5 : 9

David’s salary is 5/14th of their total salary and

John’s salary is 9/14th of their total salary.

David’s salary = (5/14) x 35000 = Rs.12500

John’s salary = x 35000 = Rs.22500

Example 2.If a : b = 3 : 5, then find (2a + 4b) : (3a + 5b) =

Solution:Dividing the numerator and denominator by b, we get

Substituting the value as

Example 3.The runs scored by Rahul and Ramesh are in the ratio of 13 : 7. If Ramesh scored 48 runs less than Rahul, then find their individual runs.

Solution:Since the ratio of the runs of Rahul and Ramesh is 13 : 7 we can take their individual scores as 13k and 7k respectively. So the difference between their score will be 13k - 7k = 6k, which is given to be 48.

6k = 48 k = 8, 13k = 104 and 7k = 56

Rahul scored 104 runs and Ramesh scored 56 runs.

Example 4.What number shall be added to or subtracted from each term of the ratio 7 : 16, so that it becomes equal to 2 : 3?

Solution:Let x be the number to be added to each term of the ratio. Then we have

⇒ 21 + 3x = 32 + 2x

x = 11. So. 11 has to be added to each term to make it 2 : 3.

Example 5.If = then find

Solution: = ⇒ x =

By substituting value of x in

we get

Variation

Two quantities A and B may be such that as one quantity changes in value, the other quantity also changes in value bearing certain relationship to the change in the value of the first quantity.

Direct Variation

One quantity A is said to vary directly as another quantity B if the two quantities depend upon each other in such a manner that if B is increased in a certain ratio. A is increased in the same ratio and if B is decreased in a certain ratio, A is decreased in the same ratio.

This is denoted as A α B (A varies directly as B).

If A α B then A = kB, where k is a constant, it is called a constant of proportionality.

For example, when the quantity of sugar purchased by a housewife doubles from the normal quantity, the total amount she spends on sugar also doubles, i.e., the quantity and the total amount increase (or decrease) in the same ratio.

From the above definition of direct variation, we can see that when two quantities A and B vary directly with each other, then NB = k or the ratio of the two quantities is a constant. Conversely, when the ratio of two quantities is a constant, we can conclude that they vary directly with each other.

If X varies directly with Y and we have two sets of values of the variables X and Y, X1 corresponding to Y1 and X2 corresponding to Y2, then, since X α Y, we can write down

⇒

Inverse Variation

A quantity A is said to vary inversely as another quantity B if the two quantities depend upon each other in such a manner that if B is increased in a certain ratio, A is decreased in the same ratio and if B is decreased in a certain ratio, then A is increased in the same ratio.

It is the same as saying that A varies directly with 1/B. It is denoted as If A α 1/B i.e., A = k/B where k is a constant of proportionality.

For example, as the number of men doing a certain work increases, the time taken to do the work decreases and conversely, as the number of men decreases, the time taken to do the work increases.

From the definition of inverse variation, we can see that when two quantities A and B vary inversely with each other, then AB = a constant, i.e., the product of the two quantities is a constant. Conversely, if the product of two quantities is a constant, we can conclude that they vary inversely with each other.

If X varies inversely with Y and we have two sets of values of X and Y. X1 corresponding to Y1 and X2 corresponding to Y2 then since X and Y are inversely related to each other, we can write down

or X1Y1 = X2Y2

SOLVED EXAMPLES

Example 1.If a : b = 7 : 2, Then = ?

Solution: Then expression =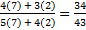

Example 2.If 4A = 5B = 7C & A + B + C = 581, C = ?

Solution: A = , B =

= 581 ⇒ C = 581 x = 140

Example 3.If 2x + 3y : 3x + 5y = 18 : 19, find x : y

Solution:

Cross Multipying

⇒ 33 = 16 ⇒

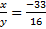
Example 4.If x : y = 2 : 3, 3x + 2y : 2y : 2x + 5y = ?

Solution:= 3x + 2y : 2y : 2x + 5y

=

= 4 : 2 : ∴ 12 : 6 : 19

Example 5.Find the fourth proportional of 3, 15, 11

Solution:3 : 15 : : 11 : x

x = (15 x 11)/3 = 55

Example 6.Find the mean proportion of 8 & 128

Solution: 8 : x : : x : 128

x2 = 8 x 128 ⇒ x = 32

Example 7.Find the third proportion of 2 & 16

Solution:2 : 16 : : 16 : x

x = (16x16)/2 = 128

Example 8Three numbers are in the ratio 3 : 2 : 5, sum of their squares is 608.

The largest of these numbers is

Solution:9x2 + 4x2 + 25x2 = 608

38x2 = 608 ⇒ x = 4, the largest is 5x = 20

Joint Variation

If there are three quantities A, B and C such that A varies with when C is constant and Varies with C when B is constant, then A is said to vary jointly with B and C when both B and C are varying i.e., A α B when C is constant and A α C when B is a constant

⇒ A α BC

A = kBC where k is the constant of proportionality.

Solved Examples

Example 1.Find the value of x, if (3x - 2) : (2x - 1)

= (4x + 8) : (7x - 2)

Solution:

⇒ (3x - 2) (7x - 2) = (2x - 1) (4x + 8)

⇒ 21x2 - 20x + 4 = 8x2 + 12x - 8

⇒ 13x2 - 32x + 12 = 0

⇒ 13x2 - 26x - 6x + 12 = 0

⇒ 13x (x - 2) - 6(x - 2) = 0 ⇒ (x - 2) (13x - 6) = 0

⇒ x = 2 or 6/13.

Example 2.If x varies inversely as (y2 - 6) and is equal to 2 when y = 16, find x, when y = 6.

Solution:x ∝

⇒ x =

At x = 2, y = 16

2 = ⇒ k = 500

x =

1.The relationship between different variables is defined to frame an equation involving the variables and the constant of proportionality.

2.One set of values of all the values of oil the variables enables as to find the value of the constant of proportionality.

3.The values of oil but one variable are given and we are asked to find the value of the one variable whose is not given

Example 3 The volume of a cylinder varies jointly as its height and the area of its base. When the area of the base is 64 sq. ft. and the height is 10 ft, the volume is 480 cu.ft. What is the height of the cylinder, whose volume is 360 cu.ft. and the area of the base is 72 sq.ft.

Solution:Let V be the volume, a = area of the base and h = height.

V = mah (m is proportionality constant)

we know, a = 64 h = 10 and V = 480

480 = m (64) (10)

⇒ m = 0.75 V = Therefore, 360 =

h = = h = ft Hence height of the cylinder is 6 ft.

Note that there should be consistency of the units used for the variables, i.e., whatever be the units used to express the variables’ when the constant of proportionality is being calculated, the same units should be used for different variables later on also when finding the value of the variable which we are asked to find out.

Example 4. , then = ?

Solution:Let each expression = k

a = (b + c) k

b = (c + a) k

c = (a + b) k

Adding all three expression

(a+b+c) = 2(a+b+c)k

1 = 2k

K = 1/2

Therefore, a = b = c hence;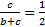

Example 5 If then find the value of expression

Solution: Let

Other Quants Notes:

• Number System
• Average
• Percentages
• Profit & Loss
• Simple and Compound Interest
• Ratio & Proportion
• Partnership
• Mixtures & Allegation
• Time, Speed & Distance
• Work, Pipes & Cistern
• Mensuration
• Geometry
• Height & Distance
• Progression
• Permutation & Combination
• Probability
• Data Interpretation